Definição: Асимптота a curva é uma reta, a qual indefinidamente se aproximando de uma curva quando você exclui ii нескінечність.
Os asymptotes verticais 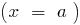
 — vertical асимптота,
— vertical асимптота,  quando
quando 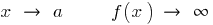
Vertical асимптота  pode ser em um ponto
pode ser em um ponto  , se o ponto
, se o ponto  limita abertas intervalos de definição de área de uma determinada função e pontos de
limita abertas intervalos de definição de área de uma determinada função e pontos de  função tende ao infinito.
função tende ao infinito.
Exemplos verticais асимптот
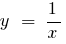
Quando 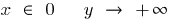
Quando 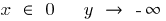
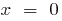 — vertical асимптота
— vertical асимптота
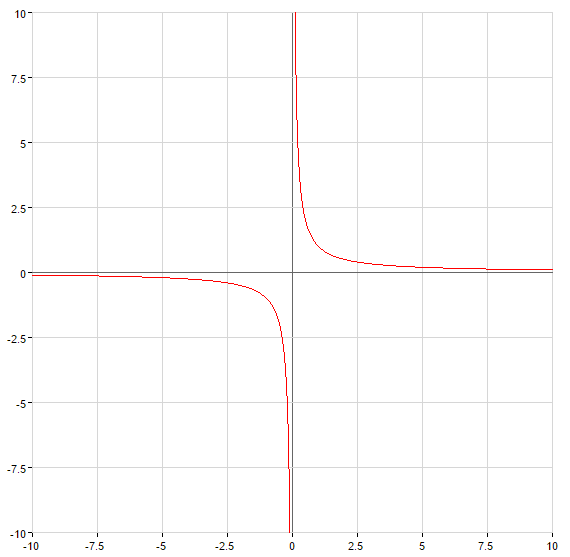
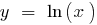
Quando 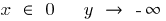
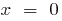 — vertical асимптота
— vertical асимптота
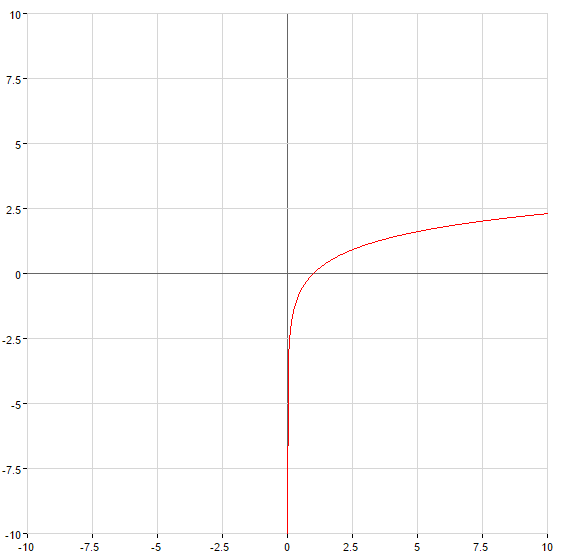
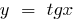
Quando 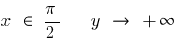
Quando 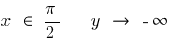
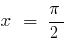 — vertical асимптота
— vertical асимптота
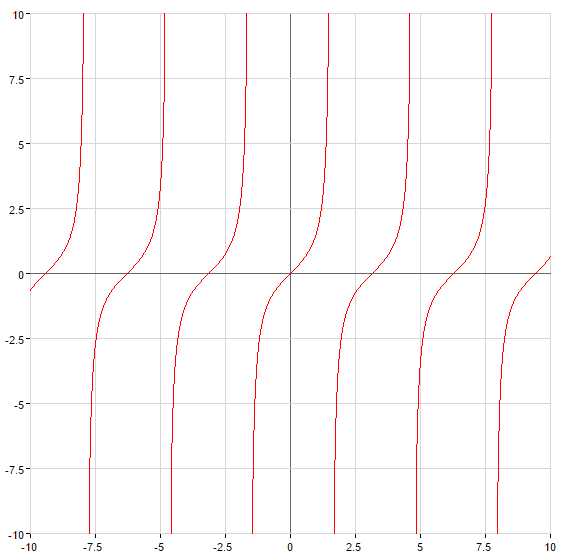
Oblíquas e horizontais os asymptotes 

- Se
 — da fracionário-racional de um recurso em que o grau do numerador a unidade de mais de grau do denominador, destacam-se a parte inteira e usamos a definição de os asymptotes.
— da fracionário-racional de um recurso em que o grau do numerador a unidade de mais de grau do denominador, destacam-se a parte inteira e usamos a definição de os asymptotes. - No caso geral, a equação inclinados e horizontais асимптот
 podem ser obtidos com a utilização de fórmulas
podem ser obtidos com a utilização de fórmulas

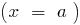
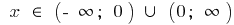
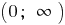
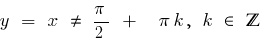

 — da fracionário-racional de um recurso em que o grau do numerador a unidade de mais de grau do denominador, destacam-se a parte inteira e usamos a definição de os asymptotes.
— da fracionário-racional de um recurso em que o grau do numerador a unidade de mais de grau do denominador, destacam-se a parte inteira e usamos a definição de os asymptotes.