定义:如果功能  上定义的时间间隔
上定义的时间间隔  ,
, 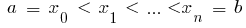 那么 一个明确组成 的功能
那么 一个明确组成 的功能  上的间隔
上的间隔  是一个数目等于限制的整体的总和,
是一个数目等于限制的整体的总和, 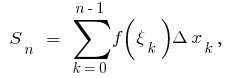 其中
其中 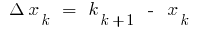 f
f 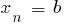
就是
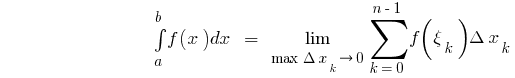
在那里 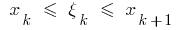 我
我 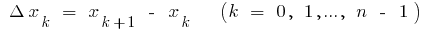
建设整体的款项的示例中确定该地区的梯形曲线
让段上  被设置为一个整体的和持续的功能
被设置为一个整体的和持续的功能 
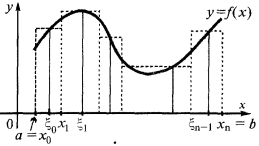
确定该区域的梯形曲线(界曲线 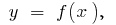 轴线
轴线 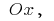 和直接,
和直接,  和
和 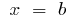 ),除切割
),除切割  要点
要点 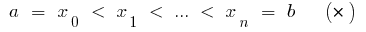
在 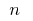 部分上选择所得到的各部分分段
部分上选择所得到的各部分分段 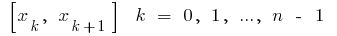 的任意一点的
的任意一点的 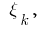 计算值
计算值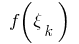 的功能
的功能  在这些点和形式的笔
在这些点和形式的笔 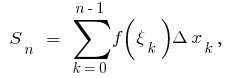 在哪里
在哪里 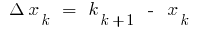
这一数额总和等于该区域的阴影矩形被称为整体的总和。
如果现在的数量分点增加了无限期的长度最大(最高)的分割分区趋于零,和价值 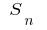 的倾向某种限制
的倾向某种限制  并不取决于该方法的划分
并不取决于该方法的划分 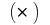 和选择的分
和选择的分 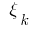 部分段,随后的价值
部分段,随后的价值 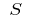 被称为区域的曲线形,即
被称为区域的曲线形,即 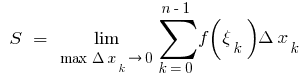
该式牛顿-莱布尼茨
如果功能  定义和持续的时间间隔
定义和持续的时间间隔  ,并
,并 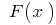 是它的组成(即
是它的组成(即 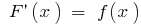 ),然后
),然后 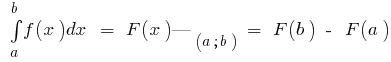
例。 作为 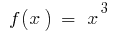 一个原
一个原 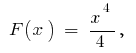 则
则 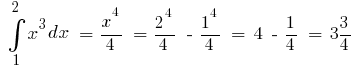
基本属性的明确的组成
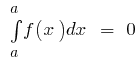
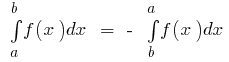
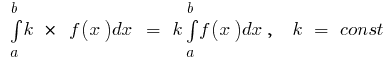
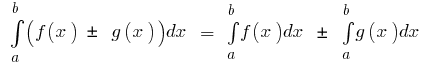
- 如果
 综合
综合  并
并 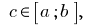 后
后
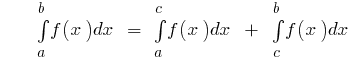

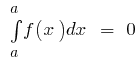
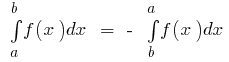
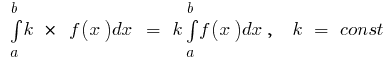
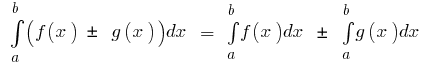
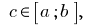 后
后