The basic laws of algebra
The square of the sum of two numbers is equal to the square of the first number plus twice the product of the first number by the second, plus the square of the second number.
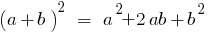
The squared difference of two numbers is equal to the square of the first minus twice the product of the first number by the second, plus the square of the second number.
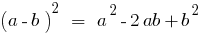
The difference between the squares of two numbers is equal to the product of the sum of these numbers is to their difference.
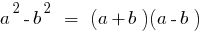
The cube is the sum of two numbers is equal to waste the first day plus triple the square of the product of the first number by the second, tripled plus the product of the first number by the square of the second plus the cube of the second number.
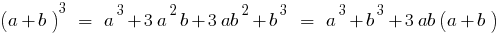
Cube of the difference is equal to the boiler of the first number minus tripled the product of the square of the first number by the second, tripled plus the product of the first number by the square of the second minus the cube of the second number.
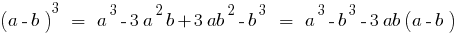
The sum of the cubes of two numbers is equal to the product of the sum of these numbers on the incomplete square of the difference of these numbers.
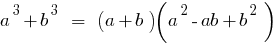
The difference between the cubes of two numbers is equal to the product of the difference of the numbers on the incomplete square of the sum of these numbers.
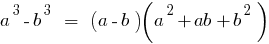
The square of the sum of multiple expressions is equal to the sum of the squares of all the summands plus all the double works of each expression for each of the following.
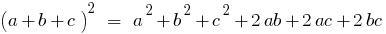
The rules of disclosure brackets
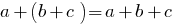
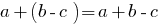
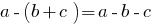
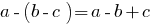
- Multiplication of a single term to the polynomial
- Multiplication of polynomial by polynomial
- The imposition of a General polynomial of the brackets
- The grouping method
- The allocation of square binomials square trinomial
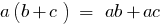
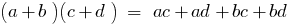
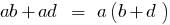
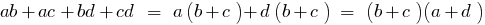
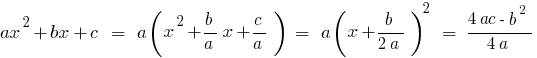
Decomposition of algebraic expressions into factors.
Square trinomial
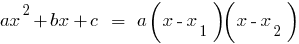
The difference of two numbers the n-th degree
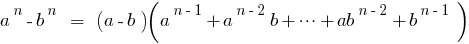
The difference between two numbers of the fourth degree
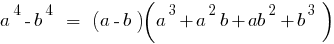
The difference between two numbers of the fifth degree
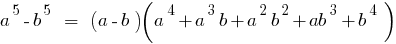
For odd integer n
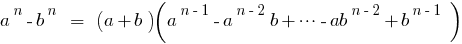
The Binomial Theorem
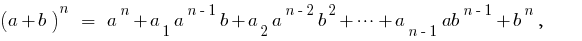where the coefficients of this decomposition 
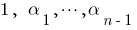can be derived from Pascal's triangle.