Definition: a Function 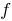 is called periodic with period
is called periodic with period 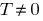 if for any
if for any 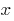 of the identifying numbers
of the identifying numbers 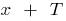 and
and 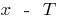 also included in the scope and
also included in the scope and
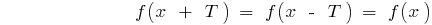 .
.
Properties of periodic functions
- If the number is
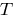 a period function
a period function 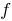 , then the number
, then the number 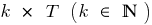 is also the period of the function.
is also the period of the function. - If the function is
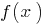 periodic with a period
periodic with a period 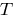 , the function
, the function 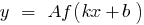 is also periodic and its period is
is also periodic and its period is 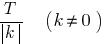
- If the function is
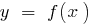 periodic with period
periodic with period 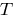 , then the composed function (function of function)
, then the composed function (function of function) 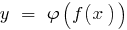 is also periodic with period
is also periodic with period 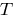 .
. - To plot periodic functions with the period
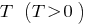 enough to graph on the interval length
enough to graph on the interval length 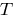 , and then in parallel to shift this graph along the axis
, and then in parallel to shift this graph along the axis 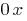 at a distance
at a distance 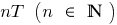 left and right.
left and right.
Examples of periodic functions
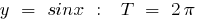
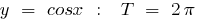
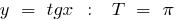
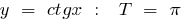

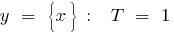
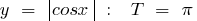
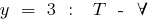

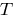 a period function
a period function 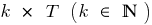 is also the period of the function.
is also the period of the function.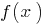 periodic with a period
periodic with a period 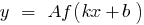 is also periodic and its period is
is also periodic and its period is 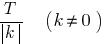
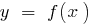 periodic with period
periodic with period 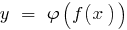 is also periodic with period
is also periodic with period 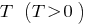 enough to graph on the interval length
enough to graph on the interval length 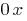 at a distance
at a distance 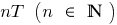 left and right.
left and right.