Decimal fraction — a fraction, the denominator of which is 10n, where n is a natural number.
Recorded decimal is read according to the scheme
| 1 | 2 | 3 | 4 | , | 5 | 6 | 7 | 8 |
| thousands | hundreds | dozens | unit | tenth | hundredths | thousands | ten |
For example the decimal fraction 10,436 read "ten four hundred thirty-six thousandths".
Among the fractions most frequently used in daily life are fractions with denominators 10, 100, 1000, etc.
For example, 10 g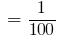 
kg,
1mm 
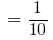cm
2cm 5mm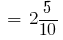 
cm, etc.
Numbers with denominators of 10, 100, 1000, etc. agreed to write without a denominator.
First write the integer part, then the numerator of the fractional part. The integer part is separated from fractional part by a comma.
For example, instead of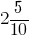 
writing 
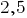(read: "2 whole and 5 tenths").
Any number that the denominator of the fractional part of which is expressed by a unit with one or more zeros can be represented in the form of a decimal.
If roll is correct, before the comma, write the number 0.
For example, instead of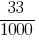 
writing 
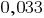(read: "as much as 0 and 33 thousand").
Pay attention! After the decimal point the numerator of the fractional parts must have the same number of digits as zeroes in the denominator.
Table of digits after the decimal point
Decimal, and any number that consists of digits (0,1,2,3,4,5,6,7,8,9).
Place each digit in the number is important: it defines the bit of the number.
The decimal fraction consists of integer part (all the numbers before the decimal point) and fractional parts (all the figures after the decimal point).
The integer part of a decimal can be divided into discharges as well as natural numbers: units, tens, hundreds, thousands, etc.
The fractional part is a decimal, divide on categories: ten (denominator fractions 10), hundredths (tenths (in the denominator of the fractions 100) thousandths (tenths (in the denominator of the fractions 1000), etc.
The table digits can be supplemented by any desired number of columns.
- 1-th digit after the decimal point — decimal,
- 2-th digit after the decimal point — discharge hundredths,
- 3-th digit after the decimal point — discharge thousandths,
- 4-th digit after the comma — category of ten,
- 5-th digit after the decimal point — the discharge of one hundred thousandth,
- 6-th digit after the comma — category of the vast
- 7-th digit after the comma — category of the ten million,
- 8-th digit after the decimal point — discharge Stalina.
Addition and subtraction of decimal fractions
To add or subtract decimals, you need to:
- To equate these fractions the number of digits after the decimal point;
- Write them under each other so that the decimal point was written under the comma;
- To perform addition (subtraction), not paying attention to the decimal point;
- To put the answer in a comma under comma in these fractions.
Example:
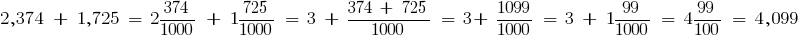
Properties of addition for decimals:
a + b = b + a - adjustable property
(a + b) + c = a + ( b + c ) - binding property
Multiplying decimals
To multiply two decimals, we must:
1. perform the multiplication, ignoring the commas
2. separate with a comma as many figures on the right, how many of them after the decimal point in both factors together.
Read more here
Dividing decimals
To divide a decimal fraction by a natural number, it is necessary:
1. to divide a fraction by that number, ignoring the decimal point;
2. to put a comma in private, when delenna a part.
Read more here
Comparing decimals
To compare two decimals, you must first call them at the number of decimal places, attributing to one of them right zeros, and then, dropping a comma, to compare the resulting positive integers.
Example:
Compare two decimals 0,642 and 0.65. Even the number of decimal places assigned to the number of 0,65 case zero. Get the fraction 0,564 and 0,650.
Write them as fractions:
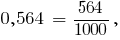
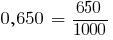
The denominators of the fractions are the same.
From two fractions with the same denominators, the larger, the fraction that has a greater numerator.
Since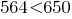 
, then 
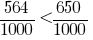, therefore,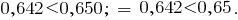 
Decimals can be compared by bits.
In decimal fractions and 26,63 6,553 enough to compare the whole parts. As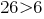 
, then ;
.
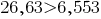Finite and infinite decimal fractions
Definition:a Finite decimal fraction is called a fraction, which contains a finite number of digits after the decimal point.
Example: 222,35
Definition: an Infinite decimal fraction is called a fraction, which does not contain a finite number of digits after the decimal point.
Example: 222,35...
Definition:an Infinite periodic decimal (periodic roll) is called a recurring decimal at the end contains a group of digits that repeat.
Example: 222,489898989...
Period of an infinite periodic decimal fraction is called the group of digits that repeat. In the previous example, is 89.
Periodic decimal fraction is called a pure periodic fraction, if her period starts immediately after the comma, and period can contain any finite number of digits.
Example: 8,44444....
Periodic decimal fraction is called a mixed fraction, if periodic decimal fraction contains a number that is placed between a part and the period. The number of recurring decimal that stands between a part and the period is called prepared this fraction.
Example: 8,4578787878...