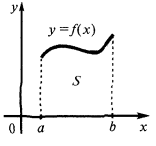
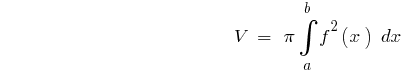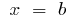Die Fläche des krummlinigen Trapezes
Die Fläche des krummlinigen Trapezes, begrenzte Zeitplan der kontinuierlichen positiven befuhr 
Funktionen,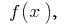 
die Achse 
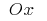und den geraden 
und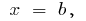 
gleich
Beispiel.Berechnen Sie die Fläche der Figur, begrenzten Linien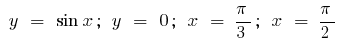 
Porträtiert diese Linie, so erhalten wir krummlinige Trapez
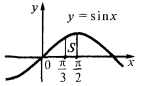
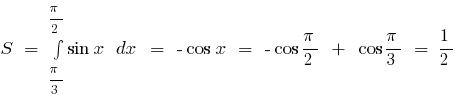
Die Fläche der Figur beschränkter Graphen von zwei Funktionen und geraden 
und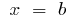 
Wenn auf einer bestimmten Strecke eine kontinuierliche Funktion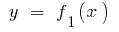 
und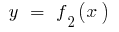 
haben dann die Eigenschaft, dass 
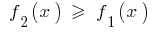für alle 
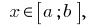etwas
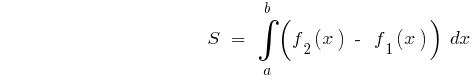
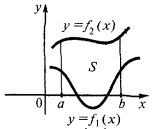
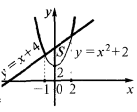
Beispiel.Berechnen Sie die Fläche der Figur, begrenzten Linien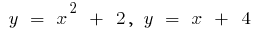 
Zeigen wir uns festgelegten Linie und der x-Punkt Ihrer Schnittpunkte.
Schnittpunkte der x-Punkt: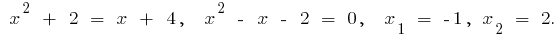 
Dann nach der Formel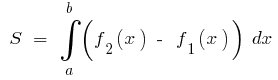 
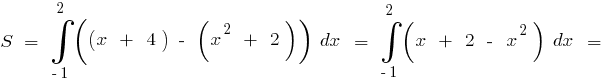
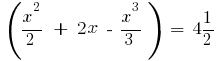
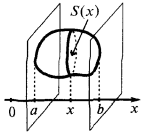
Das Volumen von Körpern
Im Allgemeinen Fall
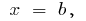Wenn der Körper liegt zwischen zwei senkrecht zur Achse der Ebenen, die durch die Punkte und dann
wo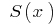 
— der Ebene der Querschnittsfläche des Körpers, die durch den Punkt 
und senkrecht zur Achse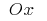
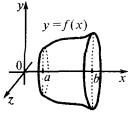
Für Rotationskörper
Wenn der Körper erhalten durch Drehung um die Achse des 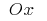krummlinigen Trapezes, die begrenzt Zeitplan kontinuierliche und невідємної Funktionen 
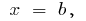auf der Strecke und geraden und dann
