परिभाषा: एक पूर्णांक  द्वारा विभाजित एक पूर्णांक
द्वारा विभाजित एक पूर्णांक  है, अगर वहाँ इस तरह के एक संख्या
है, अगर वहाँ इस तरह के एक संख्या 
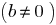 है कि
है कि 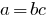 है ।
है ।
संख्या  कहा जाता है एक भाजक की संख्या
कहा जाता है एक भाजक की संख्या  , और संख्या
, और संख्या  है एक कई की संख्या
है एक कई की संख्या  .
.
गुणों की विभाज्यता
- तो
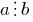 और
और 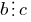 , तो
, तो 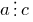 .
. - यदि
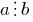 और
और 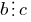 ,
,  और
और  किसी भी पूर्णांक है, तो
किसी भी पूर्णांक है, तो 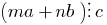 .
. - अगर
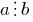 और
और 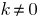 है कि
है कि 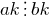 है.
है. - यदि
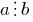 और
और 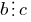 तो
तो  और
और 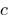 — vsampler संख्या है ।
— vsampler संख्या है ।
विभाज्यता नियम
विभाज्यता के नंबर 2
पिछले अंकों की संख्या के द्वारा विभाज्य है 2 (भी).
एक पूर्णांक  है कि विभाज्य द्वारा 2 कहा जाता है, यहां तक कि, और यह हो सकता है के रूप में प्रतिनिधित्व किया
है कि विभाज्य द्वारा 2 कहा जाता है, यहां तक कि, और यह हो सकता है के रूप में प्रतिनिधित्व किया 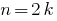 है, जहां
है, जहां 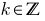 .
.
एक पूर्णांक  नहीं है कि विभाज्य द्वारा 2 कहा जाता है अजीबऔर हो सकता है के रूप में प्रतिनिधित्व किया
नहीं है कि विभाज्य द्वारा 2 कहा जाता है अजीबऔर हो सकता है के रूप में प्रतिनिधित्व किया 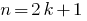 है, जहां
है, जहां 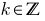 .
.
विभाज्यता संख्या के द्वारा 3
अंकों का योग 3 के द्वारा विभाज्य है.
उदाहरण के लिए, संख्या 822 है । यह शामिल नहीं करता है किसी भी ट्रिपल, लेकिन राशि के अपने आंकड़े 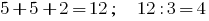 3 के द्वारा विभाज्य है, समान रूप से इसलिए विभाज्यता नियम 822 3 के द्वारा विभाज्य है
3 के द्वारा विभाज्य है, समान रूप से इसलिए विभाज्यता नियम 822 3 के द्वारा विभाज्य है 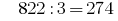 .
.
विभाज्यता नियम 10 में से
संख्या के साथ समाप्त होता है 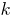 शून्य.
शून्य.
विभाज्यता की संख्या 4
संख्या के द्वारा व्यक्त की है, पिछले दो अंकों की एक निश्चित संख्या के द्वारा विभाज्य है 4.
उदाहरण के लिए, संख्या 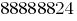 काफी बड़ी है, विभाजन के लिए छात्र 7 वीं कक्षा में है ।
काफी बड़ी है, विभाजन के लिए छात्र 7 वीं कक्षा में है ।
हालांकि potrebno केवल जरूरत है की जाँच करने के लिए विभाज्यता 4 द्वारा पिछले दो अंक 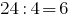 , हम कर सकते हैं निष्कर्ष है कि 88888824 एक भाजक के चार.
, हम कर सकते हैं निष्कर्ष है कि 88888824 एक भाजक के चार.
विभाज्यता की संख्या 7
नियम विभाज्यता के द्वारा 7 की बड़ी संख्या है. मानसिक रूप से तोड़ने की संख्या में ब्लॉक के तीन अंक से शुरू, पिछले अंक है । नियमों के अनुसार, यदि अंतर की राशि के ब्लॉक में खड़ा है, यहां तक कि स्थानों और योग ब्लॉक के लिए, अजीब जगहों पर खड़े बांटा गया है, 7, संख्या 7 से विभाज्य है.
उदाहरण के लिए, 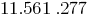
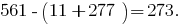
की जाँच करें 273 नियम
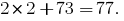
इस नंबर पर है "सुंदर" में बांटा गया है 7. तो जाँच करने के लिए विभाज्यता के एक नंबर के द्वारा 7 और उदाहरण को हल संभावना है के लिए कई नियम हैं । उनमें से प्रत्येक के एक नंबर के लिए संख्या के कुछ फायदे दूसरे के ऊपर है, तो जो रास्ता चुनना है, और अधिक सहज ज्ञान युक्त है और तेजी से.
विभाज्यता की संख्या 5
पिछले अंकों की संख्या 0 या 5.
विभाज्यता की संख्या 8
संख्या के द्वारा व्यक्त की पिछले तीन अंक की दी गई संख्या से विभाज्य है 8.
विभाज्यता की संख्या 9 से
का योग अंकों की संख्या के द्वारा विभाज्य 9.
विभाज्यता की संख्या 11 से
के बीच अंतर की राशि के अंक में खड़े अजीब जगहों (गिनती करने के लिए सही छोड़ दिया), और राशि के अंक में खड़े भी पदों (गिनती सही से छोड़ दिया करने के लिए) 11 से विभाज्य है.

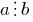 और
और 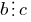 , तो
, तो 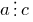 .
. और
और 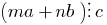 .
.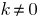 है कि
है कि 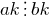 है.
है.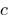 — vsampler संख्या है ।
— vsampler संख्या है ।