の定義 方程式の一変数 
の平等とは一変 
し、その形式は次の通りであると書くことはできません: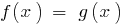 
定義 、ルート（rozvyazka)式 の値を変数の方程式の真の数値を進めていきます。
Razvesti式 手段を見つけるのルーツ(交流)又はめになることを示しています。
の許容値(odz)方程式
個人情報の定義について の許容値範囲の定義は式 —全体の範囲の機能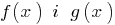 
は左右の式により求まります。
の地域の許容値(odz)
例
定的な計算式は以下の通りです。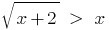 
量子力学の解釈問題をめぐる論争: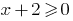 
すなわち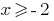 
、ドメインの機能 
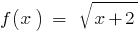が定める条件 
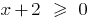にドメインの機能 
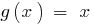はすべてリアル番号です。
方程式の調査
れらを組み合わせると、ルートの最初の方程式の根の二次方程式は、次の式と呼ばれ る結果の式です。
た場合の妥当性の平等と正確性のそれぞれ次のの、その後、adejumo 方程式の結果
そのため、利用時方程式および効果検証の根による置換の方程式のソリューションとなります。
例1
Razvesti式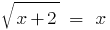 
【解決
を盛り立てて行きましょう両方の部分方程式スクエア:
;
;
;
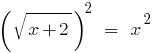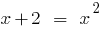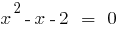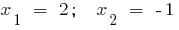ます。
なバックグラウンドチェックします。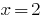 
—根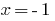 
が外部タイムをお過ごし下さい。
答え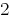 
します。
相方程式
個人情報の定義について 相当に相当)の方程式 —二つの方程式は、多くの 量子力学の解釈問題をめぐる論争 は同じ結果では、全てのソリューションの最初の方程式rozvyazka第二に、その逆も当てはまります。
一部の定理を約を均等に支配方程式のいずれか
定理1: れば一つの方程式への移動の利用規約等の規定の一部と逆の符号でお得の方程式と同等の指示するものもありますでも通知非通知を設定できます。
定理2の 場合の方程式掛算をしなければならないのは分かれ、同一の番号はゼロに等しい(同一の機能で定義されている、と等しくないゼロの ID の指定された方程式）の取得方程式と同等の、指定された。
定理3: ある場合に方程式 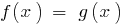を上昇(下降)が機能 
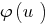しないvdbase縮小の ID の指定された方程式 
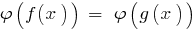に相当する、指定された( 量子力学の解釈問題をめぐる論争ます。
系の定理を約を均等に支配方程式のいずれか
結果: その機能は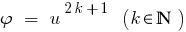 
単調増加し、
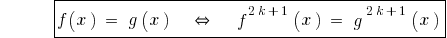ます。
の表示の両方の部分方程式の数が奇数の自然度の方程式に相当する。
結果: その機能は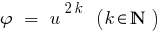 
単調増加のみの場合 
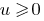の場合の両方のパーツ方程式newmn、吊り上げ、両部品の自然度の方程式に相当する。