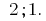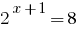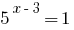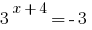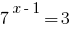دعم الحقائق
أي زيادة (انخفاض) وظيفة بين كل يكتسب قيمته إلا في نقطة واحدة من هذه الفترة.
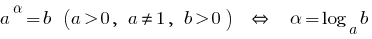
عندما 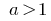 الدالة الأسية
الدالة الأسية  هو زيادة.
هو زيادة.
عندما  ....
....
عندما 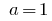 الدالة الأسية
الدالة الأسية  .
.
قرار نموذج المعادلات يجب على المرء أن يعرف خصائص من الجذور و درجة.
أمثلة حل بسيط المعادلات الأسية
الحل:
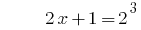
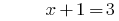
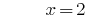
الجواب: 
الحل:
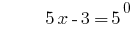
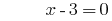
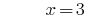
الجواب: 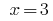
الحل:
لا جذور (حتى 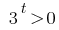 )
)
الجواب: لا جذور
الحل:
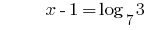
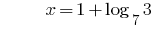
الجواب: 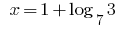
أمثلة من حل نموذج المعادلات عن طريق الحد من أبسط
______________________________________________________________________
إذا كان اليسار واليمين أجزاء من المعادلات هي توضيحية فقط من العمل ، الكسور والجذور آو حد ، فإنه من المستحسن استخدام الصيغ الأساسية في محاولة لتسجيل كلا أجزاء من المعادلة كما صلاحيات قاعدة واحدة.
______________________________________________________________________
مثال 1:
Rozwarte المعادلات 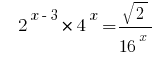 .
.
الحلول:
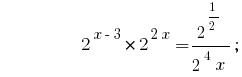
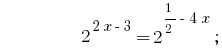
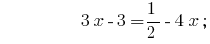
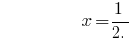
الجواب: 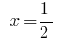 .
.
______________________________________________________________________
إذا كان جزء واحد من المعادلة الأسية هو عدد وأخرى تحتوي جميع أعضاء التعبير 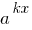 (الدعاة تختلف فقط من قبل أعضاء مجانا), هو ملائم في هذا الجزء من المعادلة أن تضع جانبا أصغر درجة
(الدعاة تختلف فقط من قبل أعضاء مجانا), هو ملائم في هذا الجزء من المعادلة أن تضع جانبا أصغر درجة  .
.
______________________________________________________________________
مثال 2:
Rozwarte المعادلات 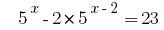 .
.
الحلول:
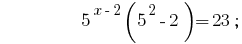
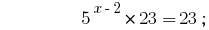
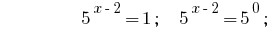
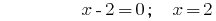
الجواب: 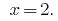 .
.
أمثلة أكثر تعقيدا المعادلات الأسية
______________________________________________________________________
تخلص من حيث العدد في الدعاة (باستخدام اليمين إلى اليسار الخصائص الأساسية من درجة).
إذا كان ذلك ممكنا ، والحد من كل درجة إلى أساس واحد وإجراء تغيير المتغيرات.
______________________________________________________________________
مثال 3:
Rozwarte المعادلات 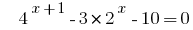 .
.
الحلول:
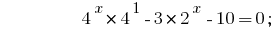
وبالنظر إلى ذلك 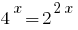 فإننا خفض درجة تلو قاعدة 2:
فإننا خفض درجة تلو قاعدة 2: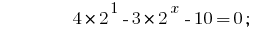
استبدال 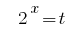 يعطي المعادلة:
يعطي المعادلة:
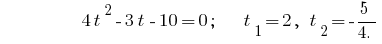
المتخلفة استبدال يعطي المعادلة 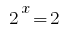 ، حيث
، حيث  أو
أو 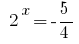 لا جذور.
لا جذور.
الجواب: 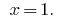
______________________________________________________________________
إن لم يكن درجة يمكن أن تخفض إلى أساس واحد ، في محاولة للحد من كل درجة إلى قاعدتين وذلك للحصول على المعادلة متجانسة.
______________________________________________________________________
مثال 4:
Rozwarte المعادلات 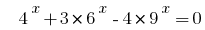 .
.
الحلول:
دعونا نعطي كل حد قاعدتين 2 و 3:
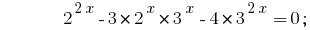
لدينا المعادلة متجانسة. عن الحل نقسم كلا الطرفين على 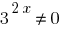 ذلك ؛
ذلك ؛
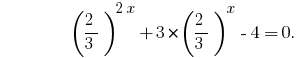
استبدال 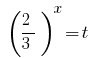 يعطي المعادلة:
يعطي المعادلة:
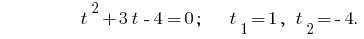
المتخلفة استبدال يعطي المعادلة 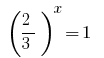 ، حيث
، حيث 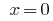 أو
أو 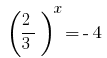 لا جذور.
لا جذور.
الجواب: 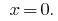
______________________________________________________________________
في حالات أخرى, نقوم بنقل جميع الشروط في المعادلة في جزء واحد و حاول أن تتحلل الحصول على التعبير في العوامل ، أو تطبيق تقنيات خاصة إلى الحل الذي نحن نستخدم خصائص وظائف المقابلة.
______________________________________________________________________
مثال 5:
Rozwarte المعادلات 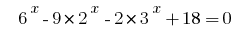 .
.
الحلول:
إذا كان في أزواج أعضاء المجموعة في الجانب الأيسر من المعادلة ، في كل زوج تبرز عامل مشترك, نحصل على :
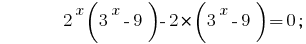
جعل بين قوسين عامل مشترك 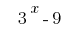 :
:
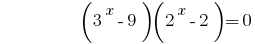
ثم 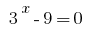 أو
أو 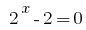 .
.
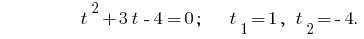
نحصل على معادلتين 1)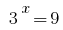 حيث
حيث  2)
2)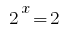 فيها
فيها  .
.
الجواب: