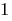Logarithmic inequality

Definition: Logarithmic inequality — inequality in which the variable is under the sign of logarithm.

So good to be able rozwiazywanie logarithmic inequality, you need to be able to control the reference ratio of the logarithm.

Equivalent transformation of simple logarithmic inequalities.

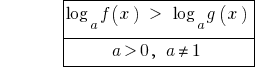
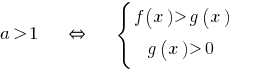
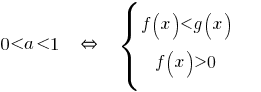
When 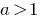the inequality sign does not change and accounted for DHS.

When

Examples of the solution of the simplest logarithmic equations

 

Example 1

Rozwarte equation: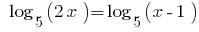

Solutions:

Since 5>1, the function 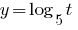is increasing and, given DHSreceived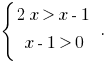

Here 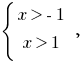it is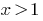

Answer: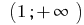

 

Example 2

Rozwarte equation: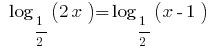

Solutions:

Since 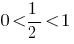, the function 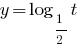is decreasing and, given DHSreceived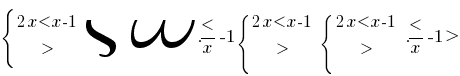

Here 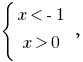is rozvytku no.

Then 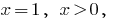that is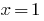

Answer: rozvytku no.

The scheme is more complex logarithmic equations

1. Using method of intervals
2. The use of equivalent transformations

As razvesti logarithmic equation

Using the formulae of logarithm and potentiating reduce the equation to a simple (consider the initial DHS and make sure not to lose roots when sujuan DHS). After transformation, if it is not possible to reduce to a simple logarithmic equations we are trying to introduce a change of variables.

Examples of the solution of logarithmic inequalities

 

Logarithmic inequality rozwadowska as well as the logarithmic equations.

Example 3 (use of formulas, logarithms)

 

Rozwarte equation: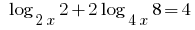

Solutions:

Going to the base 2, we get the equivalent equation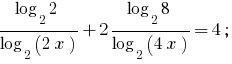

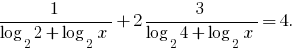
Replacement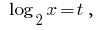

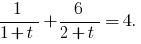
Then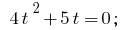

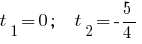
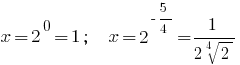
Answer: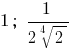

Example 4 (using properties of logarithmic functions)

 

Rozwarte equation: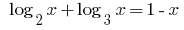

Solutions:

The function 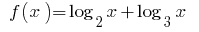increases in scope 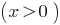as the sum of two increasing functions, and 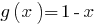comes. Therefore, the given equation has a single root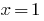

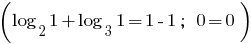
Answer: