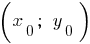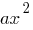Definition: a Quadratic function is called a function of the form 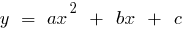 where
where 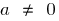
Properties of quadratic functions
- Scope
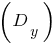
- Multiple value
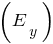
- Parity, odd parity
- Continuity and differentiability
- The increase and decrease, extrema
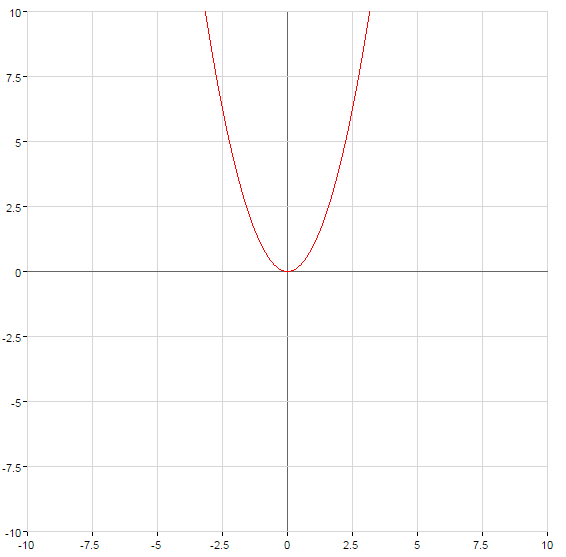
- The graph of a quadratic function is always a parabolawhose branches are directed upwards when
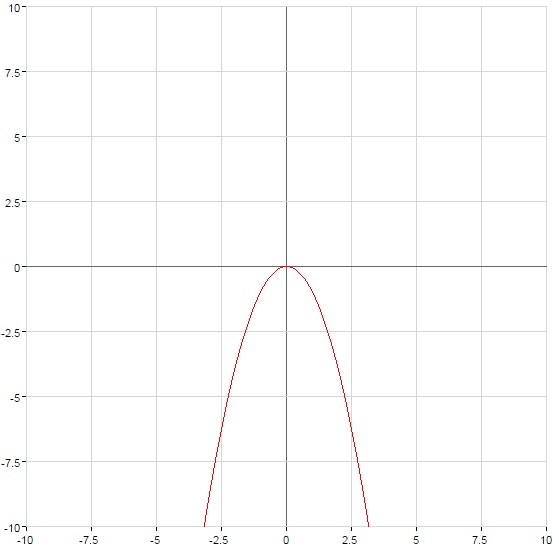
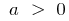 and down when
and down when 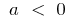
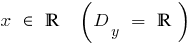
when 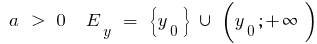
when 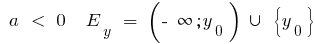
if 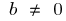 the function is neither even nor odd
the function is neither even nor odd
in 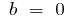 — steamroom
— steamroom
A quadratic function is continuous and diferencian on the entire number line 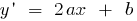
if 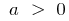 is decreasing on
is decreasing on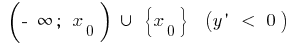 and increasing on
and increasing on 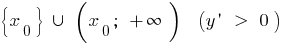 ,
, 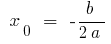 — minimum,
— minimum, 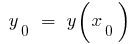 — low
— low
when 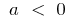 increasing on
increasing on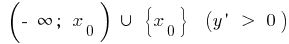 and decreasing on
and decreasing on 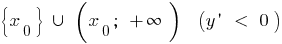 ,
, 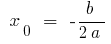 — high,
— high, 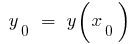 — high
— high
Coordinates of the vertex of the parabola:
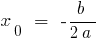 ;
; 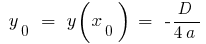 where
where 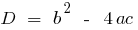
The axis of symmetry of a parabola 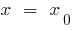
Graphs of quadratic functions


Symmetry relative to the axis 

The graph of the function is stretched 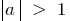 or stretched with
or stretched with 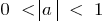 respect to the axis
respect to the axis  by the number of units equal to the number and
by the number of units equal to the number and
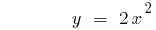
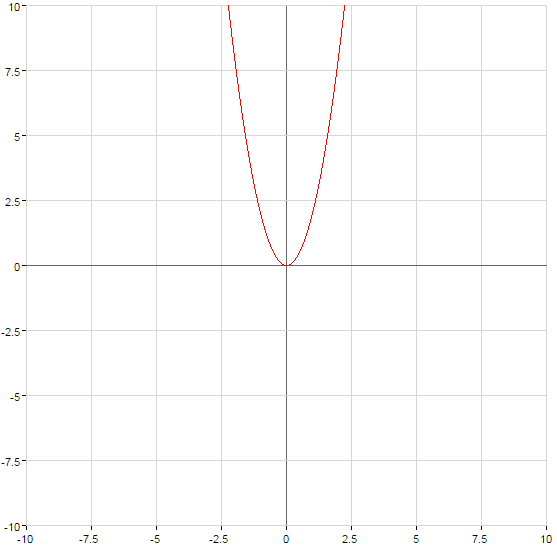
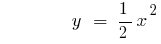
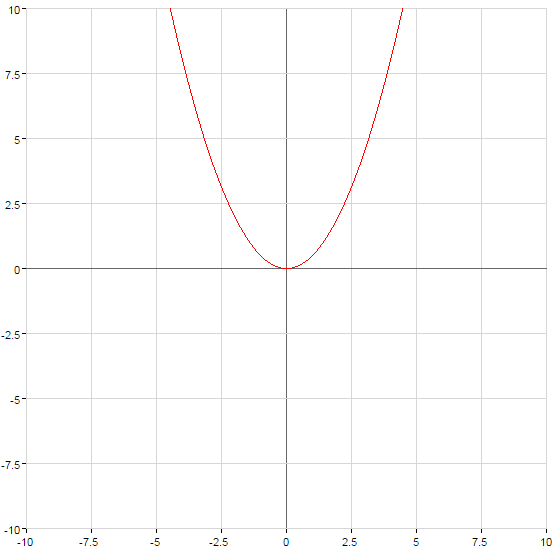
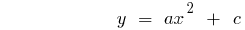
The graph of the function rises at 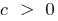 or falls with
or falls with 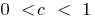 the number of units equal to the number of c
the number of units equal to the number of c
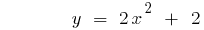
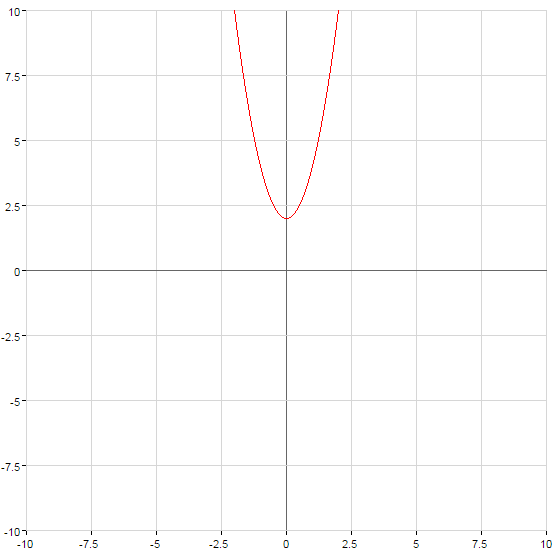
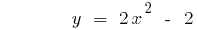
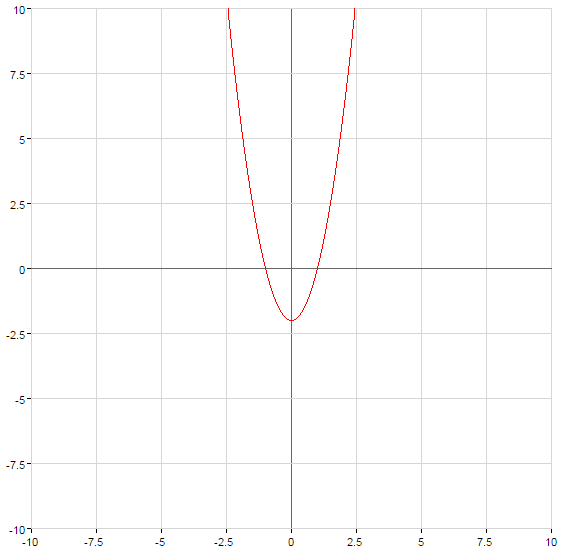
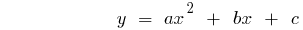
The parabola crosses the axis 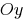 at the point C
at the point C
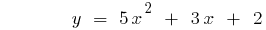
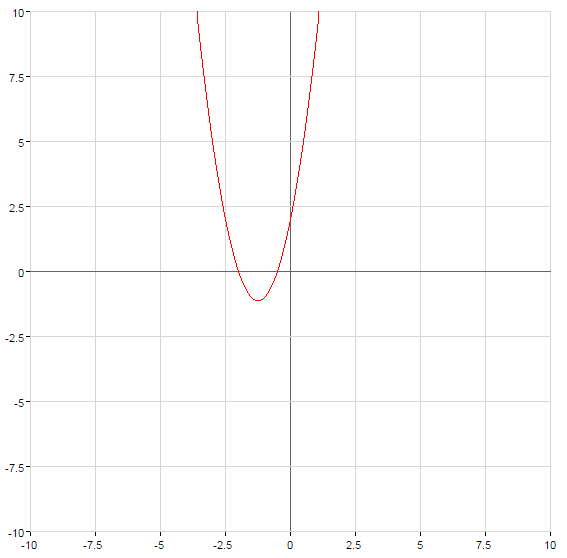
How to graph quadratic functions
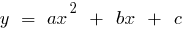
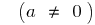
And method
- To calculate abscissa tops
- Substitute
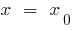 into the equation and calculate the y coordinate of the top —
into the equation and calculate the y coordinate of the top — 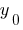
- To build a sketch of the parabola (
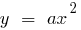 ) vertex at point
) vertex at point 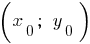
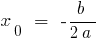
when 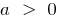 the branches up, with
the branches up, with 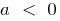 the branches down
the branches down
II method
- Razvesti quadratic equation
- Using the elementary transformations of graphs, to perform a parallel transfer of a parabola
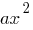
(along the axis  on
on 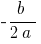 , axis
, axis 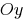 on
on 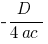 )
)

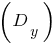
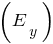
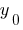
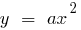 ) vertex at point
) vertex at point