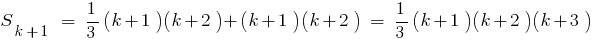Definição: uma Seqüência —variável, depende natural de um número (ou seja, a função natural do argumento).
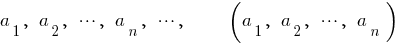 — os membros de (elementos) da sequência de
— os membros de (elementos) da sequência de
Se os elementos são números reais, então a seqüência de chamada numérico
Exemplos
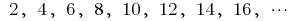 a seqüência de pares de números naturais
a seqüência de pares de números naturais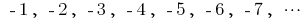 a seqüência de inteiros números negativos
a seqüência de inteiros números negativos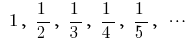 — a sequência de números, retornos aos naturais
— a sequência de números, retornos aos naturais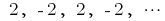 — a seqüência numérica da
— a seqüência numérica da
Crescentes e decrescentes seqüência
Definição: uma Seqüência é chamada de crescente, se cada um de seu subseqüente de um membro a mais que o anterior: 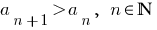 (primeira seqüência de exemplos).
(primeira seqüência de exemplos).
Definição: uma Seqüência de chamada minguante, se 
O método de indução matemática
Используеться para a prova de declarações  sobre seqüências de ou sobre expressões, dependendo natural de um número, em uma formulação que, explícita ou implicitamente, estão presentes as palavras "para qualquer natural
sobre seqüências de ou sobre expressões, dependendo natural de um número, em uma formulação que, explícita ou implicitamente, estão presentes as palavras "para qualquer natural  "
"
O esquema da prova de declarações usando o método de indução matemática
- Verificamos se esta afirmação se
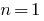 (às vezes, começando com
(às vezes, começando com 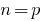 )
) - Assumimos que o verdadeiro se
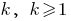 (a segunda opção — se
(a segunda opção — se 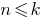 )
) - Trazemos (baseando-se na pressuposição) a validade de nossas afirmações e quando
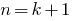
- Podemos concluir que esta afirmação é válida para qualquer natural do número de
 (qualquer
(qualquer 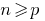 )
)
Exemplo.
Provar: 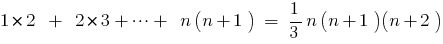
Розвязання. Para o equipamento de gravação indicado 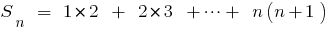
- Quando
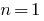 executa a igualdade
executa a igualdade 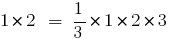
- Sugerimos que você definiu a igualdade correta quando
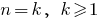 , ou seja,
, ou seja, 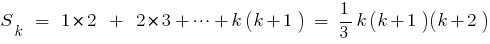
- Provar que a igualdade ocorre quando
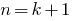 , ou seja, provar que o
, ou seja, provar que o 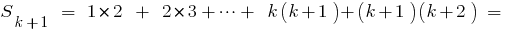
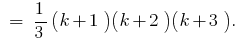
Considerando que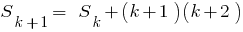 , obtemos
, obtemos 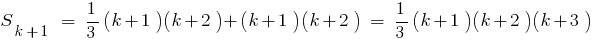
- Portanto, definida a igualdade correta para qualquer natural


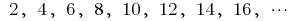 a seqüência de pares de números naturais
a seqüência de pares de números naturais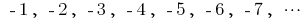 a seqüência de inteiros números negativos
a seqüência de inteiros números negativos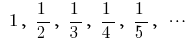 — a sequência de números, retornos aos naturais
— a sequência de números, retornos aos naturais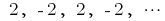 — a seqüência numérica da
— a seqüência numérica da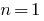 (às vezes, começando com
(às vezes, começando com 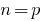 )
)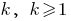 (a segunda opção — se
(a segunda opção — se 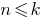 )
)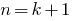
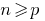 )
)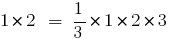
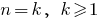 , ou seja,
, ou seja, 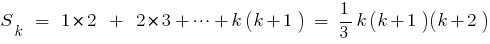
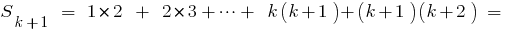
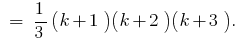
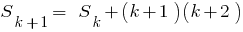 , obtemos
, obtemos