एकरसता और निरंतरता कार्यों की
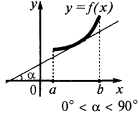
एक पर्याप्त शर्त को बढ़ाने के लिए कार्य
अगर पर प्रत्येक बिंदु के अंतराल 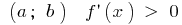 के समारोह में बढ़ रही है पर इस अंतराल
के समारोह में बढ़ रही है पर इस अंतराल
एक पर्याप्त शर्त कम करने के लिए कार्य
अगर पर प्रत्येक बिंदु के अंतराल 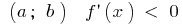 के समारोह में कम हो रही है पर इस अंतराल
के समारोह में कम हो रही है पर इस अंतराल
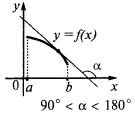
टिप्पणी. इन शर्तों रहे हैं केवल पर्याप्त है, लेकिन जरूरी नहीं स्थिति के लिए वृद्धि और घटते कार्यों
एक आवश्यक और पर्याप्त शर्त के भक्ति के समारोह
एक समारोह  है, निरंतर एक अंतराल पर
है, निरंतर एक अंतराल पर 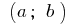 यदि और केवल यदि, जब
यदि और केवल यदि, जब  सभी अंक के अंतराल
सभी अंक के अंतराल
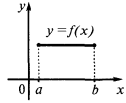
Extrema (अधिकतम और न्यूनतम) के समारोह
अधिकतम बिंदु
परिभाषा: इस बिंदु  को परिभाषित करने का कार्य करता
को परिभाषित करने का कार्य करता  है बुलाया एक अधिकतम बिंदु के इस समारोह में, अगर वहाँ
है बुलाया एक अधिकतम बिंदु के इस समारोह में, अगर वहाँ 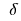 है एक पड़ोस
है एक पड़ोस 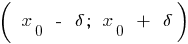 की बात
की बात  है कि सभी के लिए
है कि सभी के लिए 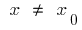 इस पड़ोस से असमानता
इस पड़ोस से असमानता 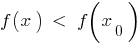
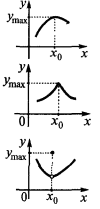
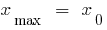 — अधिकतम बिंदु
— अधिकतम बिंदु
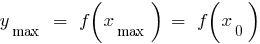 — मैक्स
— मैक्स
बिंदु की एक न्यूनतम
परिभाषा: इस बिंदु  को परिभाषित करने का कार्य
को परिभाषित करने का कार्य  कहा जाता है न्यूनतम बिंदु के इस समारोह में, अगर वहाँ
कहा जाता है न्यूनतम बिंदु के इस समारोह में, अगर वहाँ 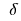 है एक पड़ोस
है एक पड़ोस 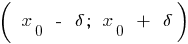 की बात
की बात  है कि सभी के लिए
है कि सभी के लिए 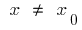 इस पड़ोस से असमानता
इस पड़ोस से असमानता 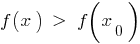
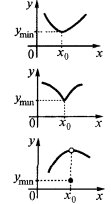
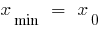 — न्यूनतम बिंदु
— न्यूनतम बिंदु
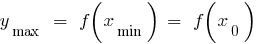 — न्यूनतम
— न्यूनतम
महत्वपूर्ण बिंदु
परिभाषा: आंतरिक अंक के डोमेन की परिभाषा के कार्यों में जहां व्युत्पन्न शून्य है या मौजूद नहीं है, कर रहे हैं कहा जाता है महत्वपूर्ण
आवश्यक शर्त के लिए एक extremum
 — extremum बिंदु
— extremum बिंदु 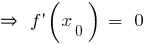 या
या 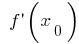 नहीं मौजूद है
नहीं मौजूद है
(लेकिन नहीं प्रत्येक बिंदु पर  जहां
जहां 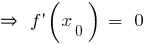 या
या 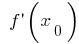 वहाँ नहीं हो जाएगा एक extremum!)
वहाँ नहीं हो जाएगा एक extremum!)
पर्याप्त शर्त के extremum
के बिंदु पर  हस्ताक्षर
हस्ताक्षर 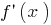 परिवर्तन
परिवर्तन 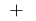 पर
पर 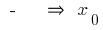 बिंदु के अधिकतम
बिंदु के अधिकतम
पर  हस्ताक्षर
हस्ताक्षर 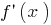 परिवर्तन
परिवर्तन 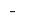 पर
पर 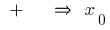 बात की न्यूनतम
बात की न्यूनतम
एक उदाहरण है एक ग्राफ की एक समारोह  है कि एक extremum
है कि एक extremum
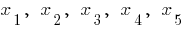 — महत्वपूर्ण बिंदु
— महत्वपूर्ण बिंदु
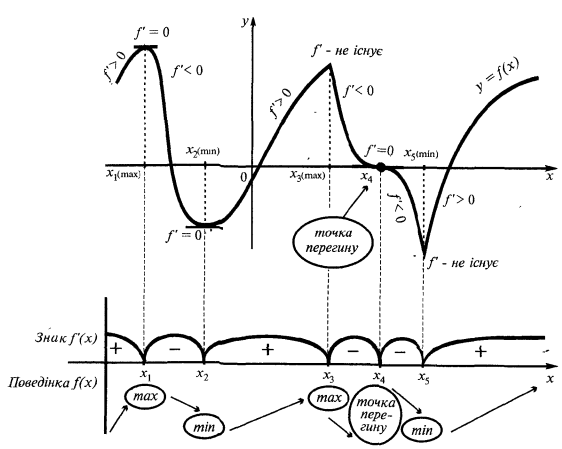
अध्ययन के समारोह के दिष्टता और extrema
उदाहरण है । 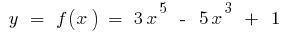
गुंजाइश: 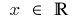
इस समारोह पर निरंतर है के हर बिंदु में अपने डोमेन की परिभाषा
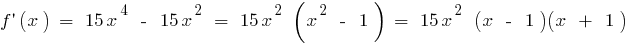
 वहाँ में है पूरी गुंजाइश
वहाँ में है पूरी गुंजाइश
 जब
जब 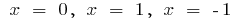
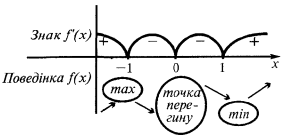
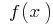 के साथ बढ़ जाती है
के साथ बढ़ जाती है 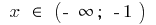 और
और 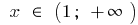
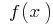 जब उतरे
जब उतरे 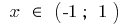
चरम अंक: 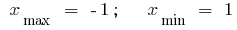
चरम सीमाओं: 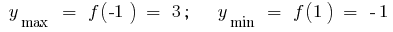
- डोमेन की परिभाषा और अंतराल पर जो समारोह है, निरंतर
- व्युत्पन्न को खोजने के लिए

- मिल महत्वपूर्ण अंक, यानी आंतरिक अंक निर्धारित करने के जहां
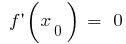 वहाँ या नहीं
वहाँ या नहीं - निरूपित महत्वपूर्ण बिंदु पर डोमेन की परिभाषा, हस्ताक्षर खोजने के व्युत्पन्न और प्रकृति के समारोह पर प्रत्येक अंतराल है, जो विभाजन की परिभाषा क्षेत्र
- प्रत्येक के लिए महत्वपूर्ण बिंदु निर्धारित है कि क्या यह उच्च या कम है या नहीं है एक बिंदु extremum
- रिकॉर्ड porni अध्ययन के परिणाम (अंतराल के दिष्टता और extrema)
अधिकतम और न्यूनतम मूल्यों के निरंतर कार्य के अंतराल पर
संपत्ति: तो इस समारोह  पर निरंतर एक अंतराल है और उसमें एक परिमित संख्या के लिए महत्वपूर्ण अंक है, तो यह उपलब्ध हो जाता, इसकी अधिकतम और न्यूनतम मूल्यों पर इस अंतराल या तो एक महत्वपूर्ण बिंदु पर करने के लिए संबंधित इस अंतराल या endpoints के अंतराल
पर निरंतर एक अंतराल है और उसमें एक परिमित संख्या के लिए महत्वपूर्ण अंक है, तो यह उपलब्ध हो जाता, इसकी अधिकतम और न्यूनतम मूल्यों पर इस अंतराल या तो एक महत्वपूर्ण बिंदु पर करने के लिए संबंधित इस अंतराल या endpoints के अंतराल
ढूँढना अधिकतम और न्यूनतम मूल्यों के निरंतर कार्य के अंतराल पर
उदाहरण है । 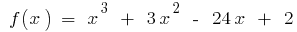 जब
जब 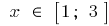
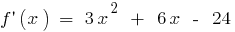
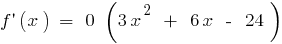 यदि
यदि 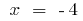 और जब
और जब 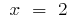
किसी दिए गए खंड के 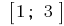 अंतर्गत आता है करने के लिए केवल महत्वपूर्ण बिंदु
अंतर्गत आता है करने के लिए केवल महत्वपूर्ण बिंदु 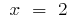
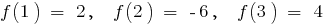

- व्युत्पन्न को खोजने के लिए

- मिल महत्वपूर्ण अंक (
 या नहीं मौजूद है)
या नहीं मौजूद है) - का चयन महत्वपूर्ण बिंदुओं के हैं कि किसी दिए गए खंड
- की गणना करने के लिए समारोह मूल्यों पर महत्वपूर्ण अंक और समापन अंतराल के
- दो मूल्यों की तुलना और चयन सबसे छोटा और सबसे बड़ा

 है कि एक extremum
है कि एक extremum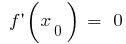 वहाँ या नहीं
वहाँ या नहीं