की अवधारणा प्रणाली और उसके rozvytku
परिभाषा: रेखीय समीकरण दो चर के साथ एक समीकरण है प्रकार की 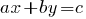 है, जहां
है, जहां  और
और  चर रहे हैं,
चर रहे हैं, 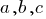 — सेट की संख्या के लिए समीकरण है ।
— सेट की संख्या के लिए समीकरण है ।
समाधान के समीकरण के साथ दो चर की एक जोड़ी है चर बदल जाता है, जो समीकरण में सही संख्यात्मक समानता है । इस जोड़ी के मान को चर कहा जाता है समीकरण को हल.
अगर दो अज्ञात मान रहे हैं एक नहीं बल्कि दो समीकरणों, तो इन समीकरणों — रेखीय समीकरण के सिस्टम के साथ दो चर.
समाधान के समीकरणों के सिस्टम के साथ दो चर की एक जोड़ी है, जो संख्या में हर समीकरण की प्रणाली में परिवर्तित कर दिया है सच्चे संख्यात्मक समानता है ।
रेखीय समीकरण के सिस्टम के साथ दो चर हल किया जा सकता है तीन तरीकों में:
- Grafone विधि को सुलझाने रेखीय समीकरण के सिस्टम में एक ही समन्वय प्रणाली के रेखांकन के दो समीकरणों और निर्देशांक के चौराहे के बिंदु के रेखांकन के अनुरूप करने के लिए जड़ों के समीकरण है. सबसे स्पष्ट तरीका है, लेकिन सबसे बड़ा गणना में त्रुटि है, क्योंकि दृढ़ संकल्प की सटीकता के निर्देशांक अंक के पैमाने पर निर्भर करता है की छवि. विशेष रूप से कठिन है, इस प्रणाली के समाधान, जब गुणांकों या समीकरण की जड़ों को आंशिक संख्या ।
- विधि लुक सबसे बहुमुखी के सभी तरीकों के रेखीय समीकरण को हल करने के साथ दो चर. यह प्रयोग किया जाता है के लिए लगभग सभी प्रकार की प्रणालियों के समीकरण है. प्रतिस्थापन की विधि यह है कि के प्रत्येक समीकरण से एक अज्ञात व्यक्त किया जाता है के माध्यम से एक और अज्ञात, और तो तब तक, जब तक आप जिसके परिणामस्वरूप समीकरण में है, जो केवल एक ही अज्ञात है ।
- विधि के बीजीय इसके अलावा अक्सर इस्तेमाल किया जाता है जब गुणांकों के एक अज्ञात संख्यानुसार बराबर या वे हो सकता है कम करने के लिए एक ही संख्यात्मक मूल्य में runoilija समीकरण के बिना जटिल गणना. विधि के बीजीय इसके अलावा प्राप्त करने के लिए है बराबर समीकरण के साथ इन में से एक रेखीय समीकरण है. दो को जोड़ने के समीकरणों आगे बढ़ना करने के लिए एक समीकरण के साथ एक अज्ञात है ।
को सुलझाने रेखीय समीकरण के सिस्टम
ग्राफिकल की विधि को सुलझाने रेखीय समीकरण के सिस्टम
उदाहरण: Rozwarte समीकरण: 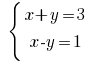
समाधान:
निर्माण रेखांकन विमान में: 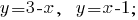
निर्माण रेखांकन के साथ रेखीय समीकरण के सिस्टम, हम देखते हैं कि रेखांकन एक दूसरे को काटना बिंदु पर एक 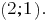
जवाब: 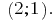
प्रतिस्थापन की विधि को हल करने के लिए रेखीय समीकरण के सिस्टम
उदाहरण: Rozwarte समीकरण: 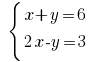
Rosv सवाना:
पहले समीकरण से हम एक्सप्रेस 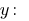
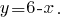
और जिसके परिणामस्वरूप अभिव्यक्ति है एवजी में दूसरा समीकरण के सिस्टम:
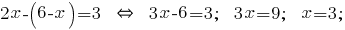
जिसके परिणामस्वरूप मूल्य  प्रतिस्थापित है अभिव्यक्ति में
प्रतिस्थापित है अभिव्यक्ति में 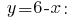
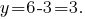
जवाब: 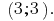
विधि के अलावा हल करने के लिए रेखीय समीकरण के सिस्टम
उदाहरण: Rozwarte समीकरण: 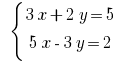
समाधान:
जरूरत से छुटकारा पाने के लिए एक चर 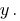 poslano गुणा पहली समीकरण की प्रणाली
poslano गुणा पहली समीकरण की प्रणाली 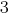 , और दूसरा –
, और दूसरा – 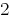 .
.
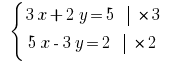
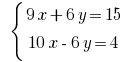
Pocino जोड़ें रेखीय समीकरण के लिए आप मिल: 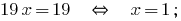
मूल्य को खोजने  के समीकरण के सिस्टम:
के समीकरण के सिस्टम: 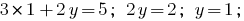
जवाब: 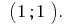
टिप्पणी: इस विधि में जोड़, गुणा कर सकते हैं पर न केवल सकारात्मक संख्या है, और नकारात्मक है ।
आप भी पा सकते हैं के बारे में जानकारी प्रणालियों के रेखीय समीकरण यहाँ
