O conceito de segunda derivada



Deixe uma função  tem derivada
tem derivada  em todos os pontos de um período. Este derivado, por sua vez, é uma função de
em todos os pontos de um período. Este derivado, por sua vez, é uma função de 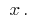 Se a função
Se a função  é diferenciado, então sua derivada é chamado de a segunda derivada
é diferenciado, então sua derivada é chamado de a segunda derivada  e indicam
e indicam 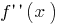 (ou
(ou 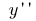 )
)
Exemplo. 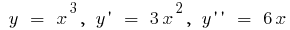
O conceito de convexidade, concavidade e pontos de inflexão do gráfico функцї
Deixe uma função  definida no intervalo
definida no intervalo 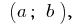 e no ponto
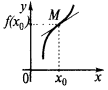
e no ponto 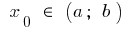 tem a final da derivada. A seguir o gráfico desta função no ponto
tem a final da derivada. A seguir o gráfico desta função no ponto 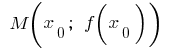 , pode passar a tangente do
, pode passar a tangente do
Se em algum bairro de pontos de  todos os pontos da curva do gráfico da função
todos os pontos da curva do gráfico da função  (exceto o próprio ponto
(exceto o próprio ponto 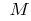 ) se encontram acima da tangente, então, diz-se que a curva (e a própria função) em um ponto
) se encontram acima da tangente, então, diz-se que a curva (e a própria função) em um ponto  é convexa (mais precisamente, é estritamente convexa). Também, às vezes, dizem que neste caso, o gráfico da função
é convexa (mais precisamente, é estritamente convexa). Também, às vezes, dizem que neste caso, o gráfico da função  é dirigida a saliência para baixo
é dirigida a saliência para baixo
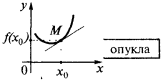
Se em algum bairro de pontos de  todos os pontos da curva (exceto o próprio ponto
todos os pontos da curva (exceto o próprio ponto  ) se encontram abaixo da tangente, então, diz-se que a curva (e a própria função) em um ponto
) se encontram abaixo da tangente, então, diz-se que a curva (e a própria função) em um ponto  é угнутою (mais precisamente, é estritamente угнутою). Também, às vezes, dizem que neste caso, o gráfico da função é dirigida a saliência acima
é угнутою (mais precisamente, é estritamente угнутою). Também, às vezes, dizem que neste caso, o gráfico da função é dirigida a saliência acima
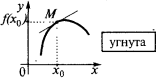
Se o ponto  no eixo dos x tem a propriedade de, ao passar um argumento
no eixo dos x tem a propriedade de, ao passar um argumento  por meio dela, a curva
por meio dela, a curva  passa por um lado tangente a outra, o ponto
passa por um lado tangente a outra, o ponto  é chamado de ponto de inflexão da função de
é chamado de ponto de inflexão da função de 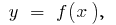 ponto de curva
ponto de curva 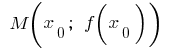 — o ponto de inflexão do gráfico da função
— o ponto de inflexão do gráfico da função 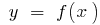
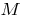 — ponto de inflexão do gráfico de uma função
— ponto de inflexão do gráfico de uma função
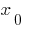 — ponto de inflexão de uma função
— ponto de inflexão de uma função
Em certa vizinhança do ponto  : quando
: quando 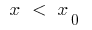 a curva abaixo da tangente, e quando
a curva abaixo da tangente, e quando 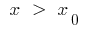 a curva acima da tangente (ou vice-versa)
a curva acima da tangente (ou vice-versa)
Estudo de funções no bojo, угнутість e o ponto de inflexão
Exemplo. 
A definição da área: 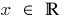
Função contínua em cada ponto de sua área de definição
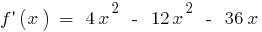
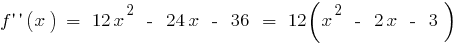
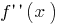 há em toda a área de definição de
há em toda a área de definição de
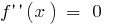 quando
quando 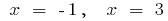
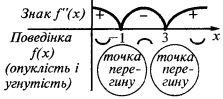
No intervalo 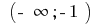 e no intervalo de uma
e no intervalo de uma 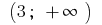 programação
programação  dirigida a saliência para baixo
dirigida a saliência para baixo 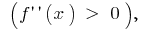 e, no intervalo de uma
e, no intervalo de uma  programação
programação  dirigida a saliência acima
dirigida a saliência acima 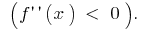
O ponto de inflexão: 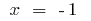 i
i 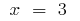 (nesses pontos,
(nesses pontos, 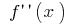 muda o sinal)
muda o sinal)
- Encontrar a definição da área e os intervalos em que a função é contínua
- Encontrar a segunda derivada
- Encontrar internos de um ponto de definição de área, em que
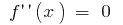 ou não existe
ou não existe - Marcar pontos obtidos na definição de área, encontrar o sinal da segunda derivada e a natureza do comportamento da função em cada intervalo, em que é dividida a área de detecção de
- Gravar o resultado de um estudo (intervalos de convexidade e concavidade e pontos de inflexão)

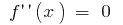 ou não existe
ou não existe