Определение простого числа
Определение: Натуральное число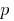 
называется простым, если у него только два натуральных делителя — само число 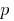и -1.
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, ... — простые числа.
Простых чисел бесконечно много.
Определение составного числа
Определение: Натуральное число называется составным, если оно имеет больше двух натуральных делителей.
6, 15, 130, ... — составные числа.
1 не является ни простым числом, ни составным.
Свойства простых делителей натуральных чисел
- Любое натуральное число (больше единицы) или делится на данное простое число
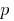, или является взаимно простым с ним. - Если произведение нескольких сомножителей делится на простое число 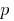, то по крайней мере один из сомножителей делится на .
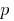- Наименьший простой делитель составного числа
не до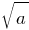 
.
.Основная теорема теории делимости
Теорема: Любое натуральное число, большее единицы, можно разложить в произведение простых чисел, причем это разложение единственное с точностью до порядка сомножителей.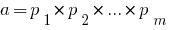
, где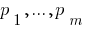 
— простые числа.
Теорема о деление с остачею
Теорема: Для любой пары чисел 
и 
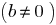существует, и притом единственная, пара целых чисел 
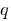и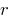 
, таких, что 
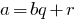, где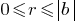 
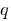( — неполное частное от деления на , 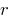— остаток от деления на ).
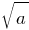